Cesta do útrob rozhodovacího stromu¶
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as pltNa úplně prvním běhu tohoto kurzu jsem vznesla požadavek “nakresli mi rozhodovací strom”. Roman pohotově vymyslel následující úlohu. Máme sadu vozidel, u kterých známe váhu a počet kol. Úkolem je vytvořit rozhodovací strom, který bude rozhodovat, zda je na vozidlo potřeba řidičský průkaz nebo není.
Na této jednoduché úloze si budeme demonstrovat, jak rozhodovací strom funguje a co všechno z něj lze vyčíst.
Začneme tím, že si vytvoříme jednoduchý DataFrame obsahující náš vozový park:
vozidla = [
{"jmeno": "jednokolka", "vaha": 20, "kola": 1, "ridicak": False},
{"jmeno": "tříkolka", "vaha": 10, "kola": 3, "ridicak": False},
{"jmeno": "odrážedlo", "vaha": 5, "kola": 4, "ridicak": False},
{"jmeno": "inline brusle", "vaha": 1, "kola": 8, "ridicak": False},
{"jmeno": "vyložený paleťák", "vaha": 140, "kola": 8, "ridicak": False},
{"jmeno": "naložený paleťák", "vaha": 1140, "kola": 8, "ridicak": False},
{"jmeno": "auto", "vaha": 2000, "kola": 4, "ridicak": True},
{"jmeno": "velorex", "vaha": 365, "kola": 3, "ridicak": True},
{"jmeno": "motorka", "vaha": 200, "kola": 2, "ridicak": True},
{"jmeno": "autobus", "vaha": 18000, "kola": 8, "ridicak": True}
]
df = pd.DataFrame(vozidla)
dfNyní si data zobrazíme, na váhy bude lepší použít logaritmické měřítko.
def show_vozovy_park(df, ax):
ax = sns.scatterplot(data=df, x="vaha", y="kola", hue="ridicak",
s=200,
ax=ax)
ax.set(xscale='log')
ax.set(ylim=(0,8.5))
ax.set(xlim=(0.5, 10**4.5))
for i, row in df.iterrows():
ax.text(1.2*row['vaha'], row['kola']+0.02, row['jmeno'])
return ax
f, ax = plt.subplots(figsize=(12,4))
show_vozovy_park(df, ax); 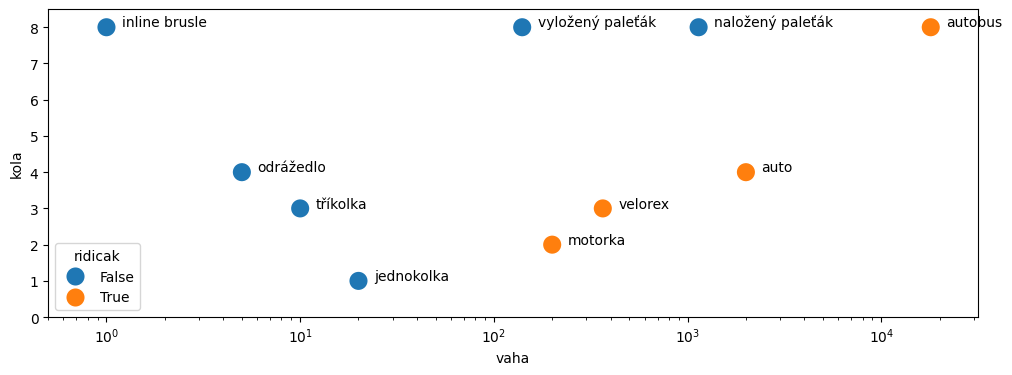
Úkol 1:¶
Prohlédněte si obrázek a zamyslete se, jak byste data odělili sadou rovných čar. Máte možnost kreslit pouze čáry kolmé na osu x (vaha) nebo na osu y (kola), tedy např. oddělující vozidla s méně než třemi koly od vozidel s více než třemi koly, apod.
Vytvoření a zobrazení stromu¶
Nyní vytvořme rozhodovací strom pomocí Scikit-learn třídy DecisionTreeClassifier.
from sklearn.tree import DecisionTreeClassifier, plot_treeinput_features = ["vaha", "kola"]
output_feature = "ridicak"
classes = ["Řidičák netřeba", "Řidičák nutný"] #False ... řidičák netřeba, True ... řidičák nutnýy = df[output_feature]
X = df[input_features]Pozn.: Tentokrát neřešíme trénovací a testovací data, jde jen o ilustrační úlohu.
tree = DecisionTreeClassifier()
tree.fit(X, y)Použijeme pomocnou funkci plot_tree a můžeme si strom prohlédnout:
_, ax = plt.subplots(figsize=(6, 7))
plot_tree(tree, proportion=True, filled=True, node_ids=True, feature_names=["vaha", "kola"],
rounded=True, impurity=False, ax=ax);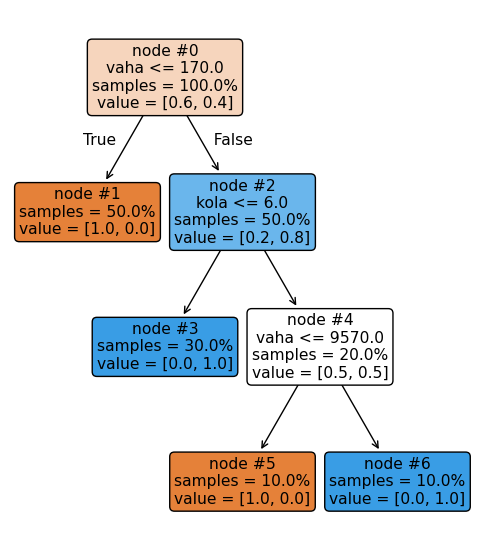
Strom na obrázku má 7 uzlů, označených #0 až #6. Uzel #0 je na vrcholu stromu a v něm rozhodování začíná. Pokud je podmínka vaha <= 170 splněna, pokračujeme doleva (uzel #1), pokud není splněna, doprava (uzel #2).
Uzel #1 je list stromu (nemá už žádné následníky) a jeho hodnota je [0.0, 1.0], kde první číslo udává příslušnost do třídy 0 (Řidičák netřeba) a druhé číslo udává příslušnost do třídy 1 (Řidičák nutný). V tomto případě, pokud skončíme v uzlu #1, nepotřebujeme řidičák.
Uzel #2 naopak obsahuje další podmínku, podle které se rozhodujeme zda pokračujeme do doleva nebo doprava. Vždy putujeme stromem tak dlouho, dokud neskončíme v uzlu, který je listem. Tento list pak obsahuje výstup.
Teď si z původního DataFramu vyzobneme jeden řádek, třeba ten pro autobus:
to_classify = df.loc[df["jmeno"] == "autobus"]
to_classifyVyužijeme metodu stromu decision_path, které předáme náš vstup (input_sample), tedy váhu a počet kol autobusu, a která nám vrátí pole nul a jedniček stejné délky jako je počet uzlů stromu. Uzly, které mají indikátor 1 jsou navštíveny při cestě stromem, přes uzly které mají indicátor 0 náš autobus neprochází.
input_sample = to_classify[input_features]
# metoda bere na vstup více vzorů (matice N x počet vstupů) a vrací matici N x počet uzlů stromu
# matice je reprezentovaná řídkou maticí, proto ji převedeme pomocí .toarray()
# v našem případě jsme předali jeden vstupní vzorek, musíme tedy vyzobnout první řádek pomocí [0]
node_indicators = tree.decision_path(input_sample).toarray()[0]
node_indicatorsarray([1, 0, 1, 0, 1, 0, 1])Teď už si jen vyzobněme čísla uzlů, které mají hodnotu indikátoru 1 a vypišme si cestu stromem:
node_ids = [i for i, indicator in enumerate(node_indicators) if indicator]
print(" --> ".join(map(lambda x: f"#{x}", node_ids)))#0 --> #2 --> #4 --> #6
Autobus tedy začíná v uzlu 0, který je vrcholem stromu a postupně postupuje stromem dle rozhodovacích podmínek v uzlech až skončí v uzlu č. 6, který je listem stromu a obsahuje výslednou klasifikaci (ověř si na obrázku, že je tomu opravdu tak).
Číslo listu, kde vzorek skončí, můžeme také získat pomocí metody apply:
leaf_id = tree.apply(input_sample)
# metoda bere na vstup více vzorů (matice N x počet vstupů) a vrací číslo listu pro každý z těchto vzorů (vektor N čísel)
# v našem případě jsme předali jeden vstupní vzorek, musíme tedy vyzobnout první číslo
leaf_id[0]np.int64(6)Teď si vypišme podrobněji cestu našeho autobusu stromem:
print(f"Pravidla pro predikci vzorku '{to_classify.iloc[0]['jmeno']}':\n")
feature = tree.tree_.feature # index vstupní proměnné, která se používá v daném uzlu při rozhodování kam dál
threshold = tree.tree_.threshold # threshold daného uzlu
values = tree.tree_.value # pro každý uzel pole výstupů pro každou třídu
for node_id in node_ids:
if leaf_id == node_id:
print(f"output node #{node_id}: ".ljust(50), end=" ")
else:
# uzel realizuje podmínku feature[node_id] <= threshold[node_id]
if input_sample.iloc[0, feature[node_id]] <= threshold[node_id]:
threshold_sign = "<="
else:
threshold_sign = ">"
print((f"decision node #{node_id} : ({input_sample.columns[feature[node_id]]} = {input_sample.iloc[0, feature[node_id]]}) " +
f"{threshold_sign} {threshold[node_id]}").ljust(50), end=" ")
# teď vypišme výstupy uzlu (lze i u vnitřních uzlů, hodnota ještě není finální)
print(f"{classes[0]}: {100*values[node_id][0][0]:3.0f}%, {classes[1]}: {100*values[node_id][0][1]:3.0f}%")
print()Pravidla pro predikci vzorku 'autobus':
decision node #0 : (vaha = 18000) > 170.0 Řidičák netřeba: 60%, Řidičák nutný: 40%
decision node #2 : (kola = 8) > 6.0 Řidičák netřeba: 20%, Řidičák nutný: 80%
decision node #4 : (vaha = 18000) > 9570.0 Řidičák netřeba: 50%, Řidičák nutný: 50%
output node #6: Řidičák netřeba: 0%, Řidičák nutný: 100%
Úkol 2:¶
Vraťte se k buňce, kde definujeme jednořádkový DataFrame to_classify a zkuste vybrat jiné vozidlo. Pak se podívejte, jak toto vozidlo putuje rozhodovacím stromem.
Zobrazení rozhodovací hranice ve vstupním prostoru¶
Na závěr si ještě prohlédneme, jak vypadá vstupní prostor a rozhodovací hranice v něm. Použijeme barevnou paletu plt.cm.coolwarm, tedy záporná čísla nám půjdou do studených barev (modrá) a kladná čísla do teplých barev (červená). Červená nám tedy indikuje potřebu řidičáku.
from sklearn.inspection import DecisionBoundaryDisplay
f, ax = plt.subplots(figsize=(12,4))
def show_decision_boundary(model, X, ax):
DecisionBoundaryDisplay.from_estimator(
model,
X,
cmap=plt.cm.coolwarm,
response_method="predict",
xlabel="vaha",
ylabel="kola",
levels=50,
eps=1,
ax=ax,
)
ax = show_vozovy_park(df, ax)
return ax
ax = show_decision_boundary(tree, X, ax)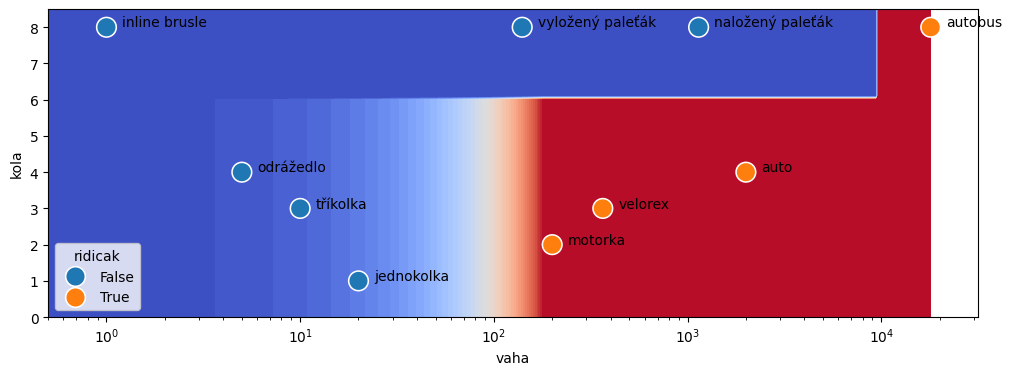
Úkol 3:¶
Na obrázku máme třídy oddělené schodovitou čarou. Dovedli byste třídy oddělit jednou čarou? Nemusí být tentokrát kolmá na osu.
Lineární klasifikace¶
Na obrázku nahoře lze oddělit vozidla bez řídičáku a vozidla se řidičákem přímkou. Klasifikaci proto můžeme zvládnout i lineárním modelem, jen pozor potřebujeme logaritmus váhy, protože na obrázku máme logaritmické měřítko.
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import FunctionTransformer
from sklearn.compose import make_column_transformerVytvoříme si transformátor, který nám sloupeček vaha převede na logaritmus. Ostatní sloupečky nechá jak jsou. Pro jednoduchost a snadné zobrazování nebudeme data škálovat.
import numpy as np
vaha_to_log = make_column_transformer(
(FunctionTransformer(np.log), ["vaha"]),
remainder="passthrough"
)Transformátor spolu s lineární regresí spojíme do jednoho modelu pomocí pipeline.
model = Pipeline([("transform", vaha_to_log), ("model", LinearRegression())])
model.fit(X, y)pred = model.predict(X)
predarray([ 0.43319275, 0.20806847, 0.05020376, -0.42921315, 0.21673647,
0.49086547, 0.83338148, 0.6782932 , 0.66691691, 0.85155464])Model se učil na datech, kde False neboli 0 znamenalo, že řidičák není potřeba, a True neboli 1 znamenalo, že řidičák potřeba je. Regrese nám bude vracet hodnoty typu float, které můžeme interpretovat tak, že hodnoty menší než 0.5 znamenají nulu, neboli bez řidičáku, a hodnoty větší než 0.5 znamenají jedničku, neboli řidičák je potřeba.
df["predikce"] = pred > 0.5
dfNa tabulce vidíme, že regrese zvládá oddělit vozidla s řidičákem a bez. Ještě si vykresleme, jak vypadá z pohledu regrese vstupní prostor.
Kromě barevné mapy si vykreslíme i čáru, zobrazující hranici tříd, tedy přímku, kde lineární regrese dává výstup 0.5. Linární regrese počítá lineární kombinaci svých vstupů, tedy:
kde je logaritmus váhy vozidla, je počet kol a jsou parametry modelu. Abychom do grafu mohli vykreslit dělící přímku, vyjádřeme si závislost váhy na počtu kol pro výstup :
Pomocí tohoto vzorečku si můžeme nagenerovat data pro vykreslení přímky odpovídající hranici.
# decision boundary display aplikovaný na celou pipeline zkresluje hranice kvůli logaritmickému měřítku a malému rozlišení
# pro větší rozlišení se to seká, logaritmické rozlišení asi neexistuje :)
# tak to pro účely obrázku obejdeme ... přidáme sloupeček vaha_log a vyzobneme linearni regresi z pipelinedf["vaha_log"] = np.log(df["vaha"])
X_plot = df[["vaha_log", "kola"]]
linear_model = model.named_steps["model"]
linear_modelf, ax = plt.subplots(figsize=(12, 4))
DecisionBoundaryDisplay.from_estimator(
linear_model,
X_plot.values,
cmap=plt.cm.coolwarm,
response_method="predict",
xlabel="vaha_log",
ylabel="kola",
levels=50,
eps=0.5, ax=ax)
sns.scatterplot(data=df, x="vaha_log", y="kola", hue="ridicak", s=150)
for i, row in df.iterrows():
ax.text(row['vaha_log']+0.2, row['kola']+0.02, row['jmeno']);
# Vykreslíme i hranici, kde lineární regrese dává na výstup přesně 0.5
# koeficienty regrese
w = linear_model.coef_
b = linear_model.intercept_
# w_0 * vaha_log + w_1 * kola + b = 0.5 --> vaha_log = (0.5 - w_1 * kola - b) / w_0
y_vals = np.linspace(0.5, 8.5, 100)
# spočti y pro hranici (predikce = 0)
x_vals = (0.5 - w[1] * y_vals - b) / w[0]
# Plot
ax.plot(x_vals, y_vals, 'k--', label='Decision boundary (y=0)');
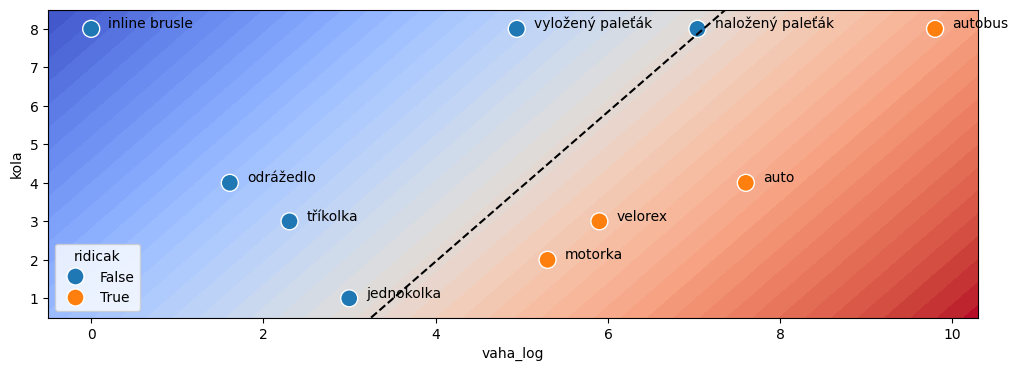
Vidíme, že naložený paleťák má sice trošku namále, ale všechna vozítka jsou správně oddělena. Pokud by se jednalo o skutečnou klasifikační úlohu s více daty, mohli bychom prahem (který je teď 0.5) hýbat a pravidla pro klasifikaci do třídy 1 zpřísňovat nebo naopak polevovat.
Dělící přímka by se pak na obrázku posouvala směrem do červené nebo modré.
Bonus: Nelineární problém¶
Pokud budeme mít data, kde nefunguje lineární klasifikace ani např. rozhodovací strom, můžeme sáhnout po modelech SVM (Support Vector Machine).
Ilustrujme si to na klasifikaci dvou spirál, umělém, ale záměrně záludném problému. Načteme a zobrazíme data.
df = pd.read_csv("2sp.txt", sep=r'\s+', header=None)
df.columns = ["x1", "x2", "class"]
df.sample(10)sns.scatterplot(data=df, x="x1", y="x2", hue="class");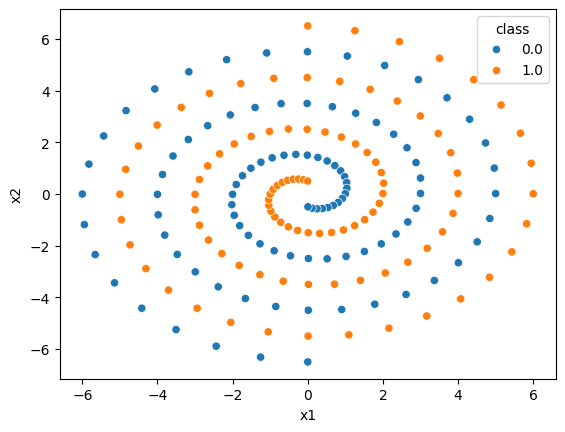
Je jasné, že lineární regrese nám tady nepomůže, zkusme co udělá rozhodovací strom.
X = df[["x1", "x2"]]
y = df["class"]model1 = DecisionTreeClassifier().fit(X, y)DecisionBoundaryDisplay.from_estimator(
model1,
X,
cmap=plt.cm.coolwarm,
response_method="predict", levels=50);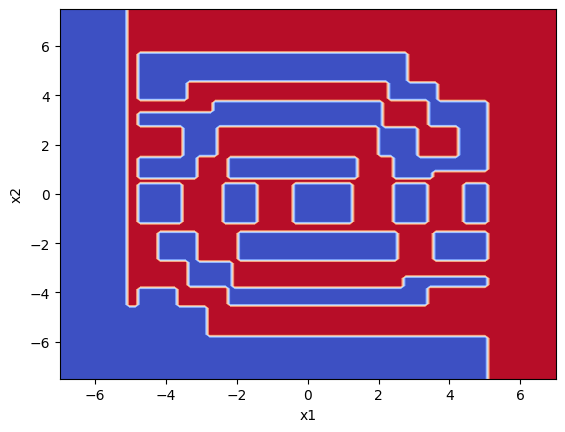
Není to úplně špatné, náznak spirál vidíme, ale ještě by se to dalo vylepšit. Podívejme se tedy, co udělá SVM Klasifikátor.
from sklearn.svm import SVC
model2 = SVC(kernel="rbf", gamma=0.8, C=10.0, probability=True).fit(X, y)
model2fig, ax = plt.subplots()
DecisionBoundaryDisplay.from_estimator(
model2,
X,
cmap=plt.cm.coolwarm,
response_method="predict_proba", ax=ax, levels=50);
sns.scatterplot(data=df, x="x1", y="x2", hue="class", ax=ax);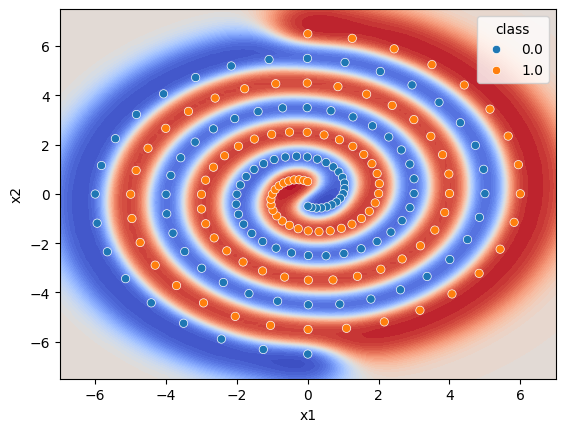
To už je jiné kafe. Trošku jsme ale podváděli, a vycucali si z prstu hyper-parametry modelu. Ano, s těmi je třeba si pohrát.
Regularizační parametr C¶
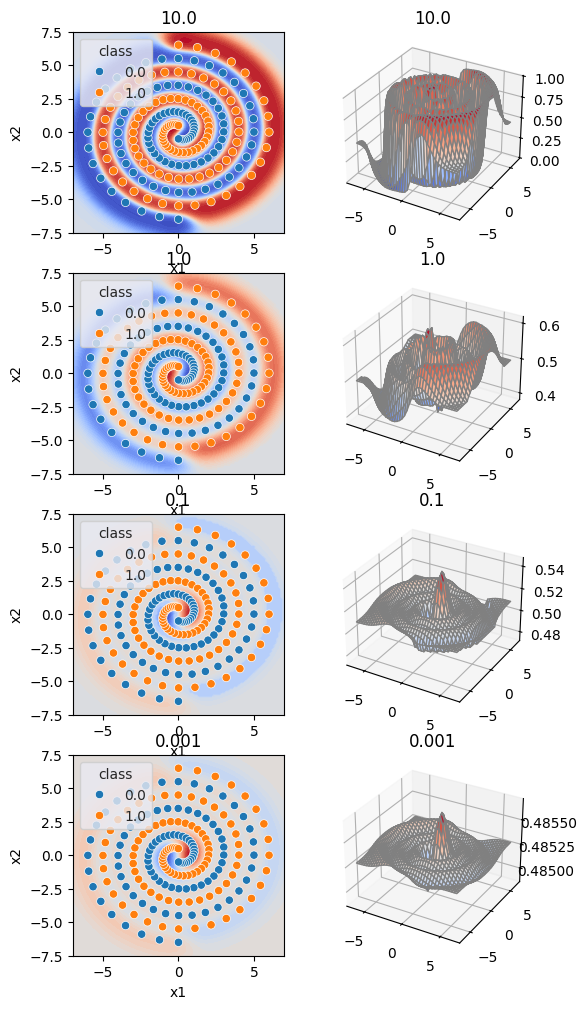
Paremetr C potkáváme u modelů často. Je to tzv. regularizační parametr, čím menší hodnota, tím více regularizujeme. A zjednodušeně řečeno, čím více regularizujeme, tím je výsledná funkce modelu (pokud nemáš ráda matematiku, vzpomeň si na úvodní ilustrační příklad a nahraď slovo funkce slovem krajina) méně divoká.
Aby sis to mohla lépe představit, vytvořme si sadu obrázků pro různé hodnoty parametru C. Nalevo vidíme klasifikaci bodů v rovině, napravo funkci modelu jako 3D grafu.
def plot(model, ax, C):
sns.set_style('darkgrid')
x_plot1 = np.linspace(-6.5, 6.5, 40)
y_plot1 = np.linspace(-6.5, 6.5, 40)
def comp(x1, x2):
input_batch = pd.DataFrame()
input_batch["x1"] = x1.ravel()
input_batch["x2"] = x2.ravel()
return model2.predict_proba(input_batch)[:, 1].reshape(40, 40)
plot1, plot2 = np.meshgrid(x_plot1, y_plot1)
plot3 = comp(plot1, plot2)
ax.plot_surface(plot1, plot2, plot3, cmap=plt.cm.coolwarm, edgecolor='gray');
ax.set_title(f"{C}");
def plot2(model, X, ax, C):
DecisionBoundaryDisplay.from_estimator(
model,
X,
cmap=plt.cm.coolwarm,
response_method="predict_proba", ax=ax, levels=50);
sns.scatterplot(data=df, x="x1", y="x2", hue="class", ax=ax);
ax.set_title(f"{C}");
C_values = [10.0, 1.0, 0.1, 0.001]
fig = plt.figure(figsize=(6, len(C_values)*3))
N = len(C_values)
axs = [[] for _ in range(N)]
rows = N
cols = 2
for i in range(N):
axs[i].append(fig.add_subplot(rows, cols, i*2+1))
axs[i].append(fig.add_subplot(rows, cols, i*2+2, projection='3d'))
for i, C in enumerate(C_values):
model2 = SVC(kernel="rbf", gamma=0.8, C=C, probability=True).fit(X, y)
plot(model2, axs[i][1], C)
plot2(model2, X, axs[i][0], C)